06. Strategy 2: Only Choice
Insight: Every unit must contain exactly one occurrence of every number
So, these are the values we obtain when we apply the function eliminate.
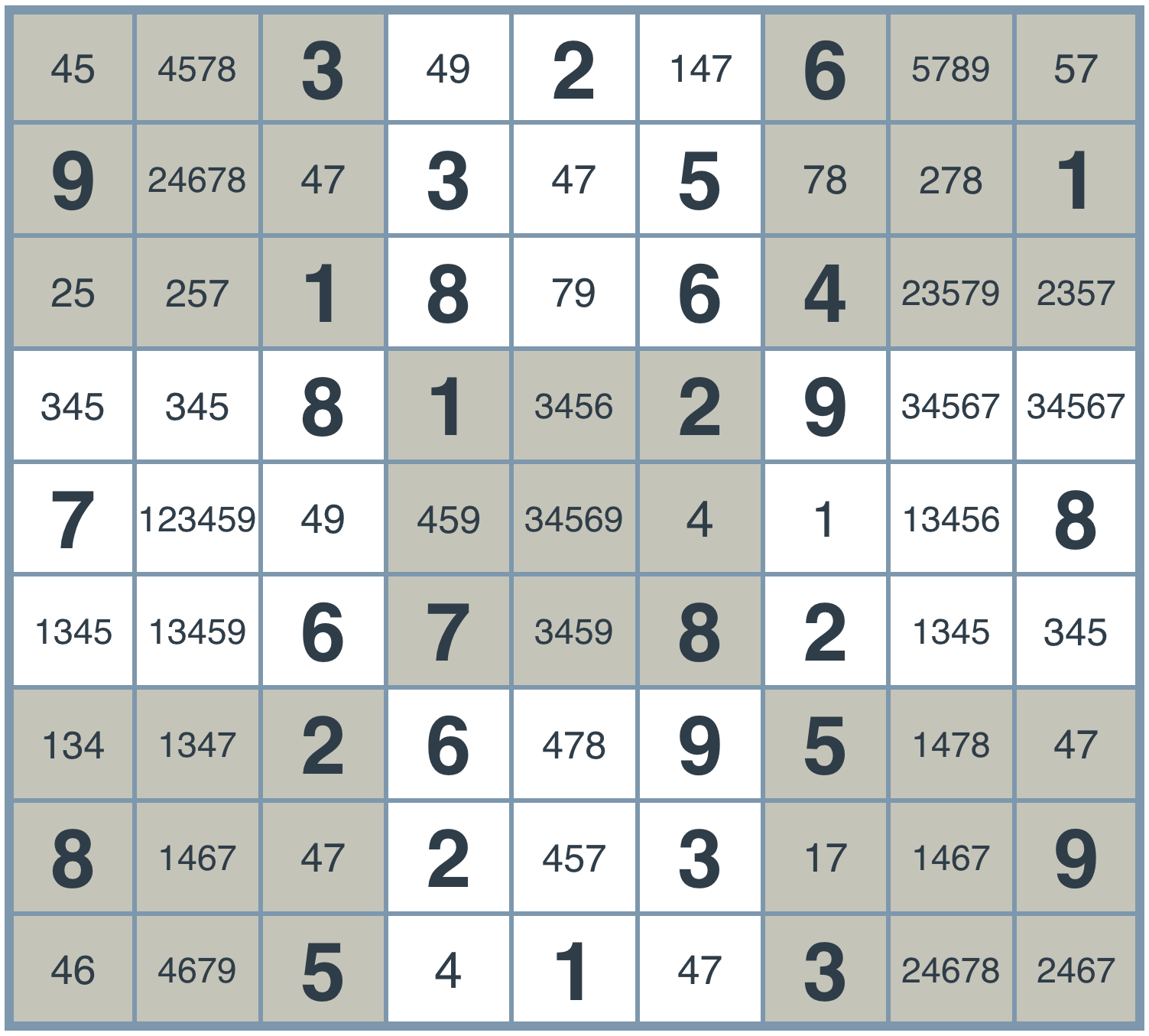
Let's actually look more carefully at the top 3x3 square in the center, highlighted in red.
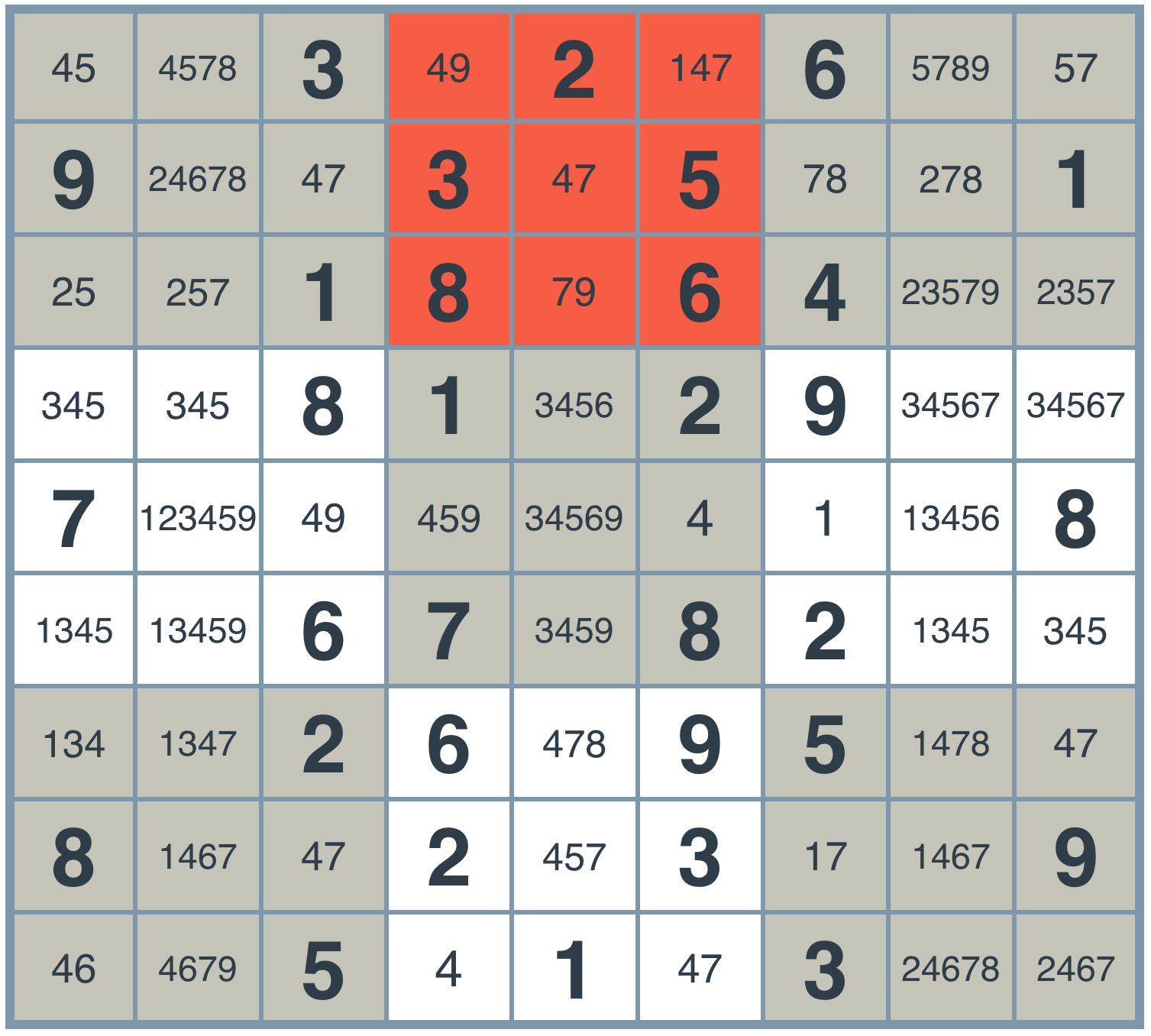
Single possibility quiz
SOLUTION:
- 1
Yes! In this unit, there seems to be only one box which would allow a value of 1 (explained below). Since each digit must appear somewhere in the unit, we conclude that the top right box must contain the digit 1.
Only Choice
So, we have another strategy!
Strategy 2: Only Choice
If there is only one box in a unit which would allow a certain digit, then that box must be assigned that digit.
Time to code it! In the next quiz, finish the code for the function only_choice, which will take as input a puzzle in dictionary form. The function will go through all the units, and if there is a unit with a digit that only fits in one possible box, it will assign that digit to that box.
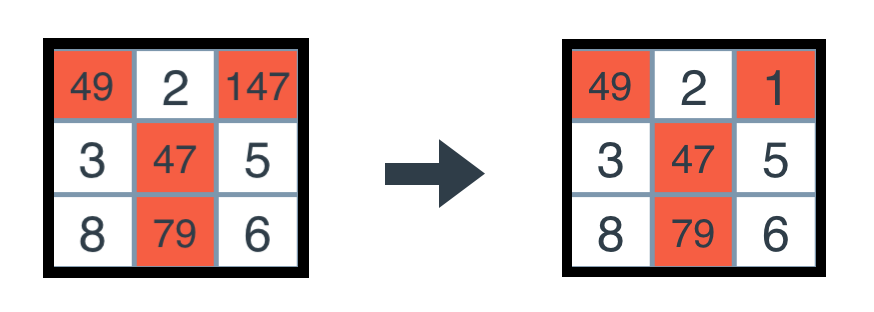
The above image shows the result of applying the only choice rule.
Start Quiz:
User's Answer:
(Note: The answer done by the user is not guaranteed to be correct)